RoonBridge Pi 5 Ubuntu 24 HDMI

Here's a fix that maybe 4 other people on earth will need.  I had this happen on Ubuntu 24.10, but it's quite possible if you attempt to install Roonbridge on 24.04 (LTS) you'll have the same issues, depending on exactly when you reboot.  To be honest, I'm not 100% sure of why the problem occurs.  I think it's a timing/race condition, but it could also just be bad code. The instructions below should fix things either way. 

Requirements: Ubuntu 24.x, RoonBridge 1.8 (build 1124 stable) and a Raspberry Pi 5. 

Symptoms:  After following installation instructions for RoonBridge playback via HDMI will cause Roon to skip through several tracks before saying "Too many errors." 

Cause: 

The issue has to do with the device description strings RAATServer caches in /var/roon/RAATServer/Settings.  Since a Pi 5 has 2 HDMI ports, you'll find at least 2 JSON files here named device_(some big string).json.  If you have a USB device connected you may find more, so be careful your files are HDMI related before editing.  In Ubuntu 24 you'll see the string vc4hdmi, which is how you can tell you aren't editing the wrong kind of file.  In any event, it's a simple edit once you know what the issue is.  

Here's the first version of my JSON:

 {"unique_id": "617c2b7a-8bf6-18d6-0243-1e918a7e673c", "external_config": {}, "output": {"name": "vc4-hdmi-1", "type": "alsa", "device": "hw:CARD=vc4hdmi1,DEV=0", "dsd_mode": "none"}, "volume": {"type": "alsa", "device": "hw:CARD=vc4hdmi1,DEV=0"}} 

The problem is the device name should be hdmi:CARD....  As I mentioned, in some cases this may already be correct and you don't need to change a thing. 

Fix: 

Make sure you have rebooted at least once after ALSA library installation.  

Just replace the hw: string highlighted above with hdmi: and you'll be playing 32 bit music through your HDMI port.  Here's a finished version: 

 {"unique_id": "617c2b7a-8bf6-18d6-0243-1e918a7e673c", "external_config": {}, "output": {"name": "vc4-hdmi-1", "type": "alsa", "device": "hdmi:CARD=vc4hdmi1,DEV=0", "dsd_mode": "none"}, "volume": {"type": "alsa", "device": "hdmi:CARD=vc4hdmi1,DEV=0"}}

  After these edits:

sudo systemctl restart roonbridge 

What happened: 

hw:CARD is the raw device name but hdmi:CARD is the ALSA virtual device.  The big issue is that RAATServer talks PCM but the raw device does not.  The raw device only talks IEC958.  In order to talk PCM (S16_LE, S24_LE, etc.) through HDMI the RAATServer should use the virtual device which has the built in PCM to IEC958 translation goodness. 

Since you have 2 HDMI devices you might as well fix both files now.   Once you make these changes you'll notice the Roon DSP features like upsampling become available. 

Why it happened: 

This is an error during RoonBridge installation storing the raw device name instead of the virtual device name.   It may be a race condition during installation, in the period between when the virtual devices get instantiated by the kernel and the RoonBridge scans the hardware or it could be bad installation code.  It's possible the "fix" is a change to the installation instructions, to explicitly reboot after installing ALSA but before installing RoonBridge.  I'll leave that up to Roon.

Alternative Installation Guide

As mentioned, a possible solution to this when installing a fresh Ubuntu 24 is to apt install alsa  and then do a reboot BEFORE installing RoonBridge.

The theory why this might work is that just installing ALSA doesn't instantiate the virtual devices.  That is, after apt install alsa the hdmi:CARD devies don't exist yet, because those get created each time the kernel starts up and not when the library is installed.  By rebooting post-ALSA installation the hdmi:CARD virtual devices should exist and therefore, hopefully, the RoonBridge install will see them.  If not, go through the steps above.   Note that this only works during installation.  What I do know is that once the device files are bad reboots alone won't fix the issue.

It's quite possible a number of Pi 5/Ubuntu/Roon users accidentally did this right, or somehow installed ALSA, rebooted and perhaps re-installed Roonbridge from scratch.  So for those people this bug wouldn't occur.   On the other hand, if you are trying to quickly stand up a minimum installation you really might not have.  In my case I rebooted after a full upgrade but before the ALSA libraries  were installed, so I suspect that's what kept things from working correctly. 

Future Proofing

As mentioned or implied, above, I'm not sure when these files get crated or recreated, but to be sure the hdmi:CARD devices exist before RoonBridge starts you'll need to add  an override to the RoonBridge service.   There seems to be a difference in the startup sequence between Ubuntu 24.04 and 24.10 so this may be particularly important in 24.10.  In any event, better safe than sorry.  Let's force RoonBridge to wait for audio and networking to be done before starting.  This way any future rewriting of these files by RoonBridge should hopefully happen in the right order. 

First:  

sudo systemctl edit roonbridge 

Add these lines: 

[Unit]
Description=RoonBridge
After=sound.target
After=network-online.target

 

Save and reboot.   This will ensure that RoonBridge always starts after sound.target and the network is on.  Hopefully then that means that future installations or updates will only recreate those JSON device files correctly.  Who knows, this may also solve issues about USB DACs being discovered by RoonBridge or not after a reboot.

You are welcome.  

Discerning or Hard to Drive Speakers

Speaker impedance is a complicated subject, but it is well known that some speakers are harder to drive than others.  Sometimes there is a legitimate reason for this and sometimes a difficult impedance curve appears to be a marketing gimmick.   We'll cover the basics of impedance curves, but what I want you to keep in mind is that a decent crossover designer CAN make an impedance much worse than it should be.  A bad crossover designer can achieve the same.

I want to emphasize, that in some cases you can make the speaker much harder to drive, without changing the speaker's frequency response with an ideal voltage source.   By doing so you have artificially created a speaker that is "highly discerning" of amplifiers specifically because amplifiers are not ideal voltage sources.  They have limits based on the size of the power supply and output stage capacity, as well as use of feedback. 

No two speaker models have the same impedance curve, the lower the impedance, and wider the "phase angle" the harder they are to drive.  Phase angle means whether the voltage leads (inductive) or lags (capacitive) the voltage across a device.   

A "hard to drive" speaker requires an amplifier with more current, and these amplifiers are usually more expensive than you would need for an "easy load."  

The Physics

An impedance curve is a measure of the impedance of a loudspeaker at a variety of frequencies.  In the worst  case this curve will interact with the amplifier, causing the output frequency response to "track" or mimic  the impedance curve.  Where the impedance is high, the output is high, where it's low the output is low.  The published frequency response measurements in Stereophile are always conditional on the amplifier being well in it's comfort zone. 

 

This is essentially the common limiting factor of tube amps (yeah, not ALL tube amps) and why some speaker makers like Fritz go out of their way to produce speakers which are easy to drive across their entire range.

 

The Gimmick

Many audiophiles unfortunately believe that a speaker that shows the difference between upstream components is more musical or easy to listen to.  They are not.  They just show differences better, but these buyers will prefer the speaker that is harder to drive, and then buy a bigger amplifier.  

The way this gimmick works is that a buyer, hopefully a well-heeled audiophile, is tricked into buying speaker A instead of B because they believe it to be more "discerning."  When you use a $1,000 amp and then swap it for a $30,000, 200 lb gorilla of an amp the speaker suddenly comes alive.  Clearly, this speaker can hear all the great improvements between the first amp and the second, and therefore, the "discerning" speaker is going to reveal more about the music than any other.  This also justifies buying monoblock amplifiers when you'd otherwise be happy with a small integrated had you picked an easier to drive speaker.

A speaker that is hard to drive causes a softening of output where the impedance is low.  For instance, with an ESL tube amps often sound dull, and lacking treble. Swap to a nice solid-state and they bloom.  Even a speaker with a mid-bass around 3 Ohms that is otherwise clean may make current delivery audible. 

To be clear, there is absolutely no proof that a "discerning" speaker is actually better at playing real music, so this false logic is part of the whole inference chain.  

Just like with romantic partners, a high-maintenance partner is just a high-maintenance partner, that doesn't make them smarter, funnier or more responsible at picking up the kids every day.  

The Bad

Some speakers are by the nature of their physics never going to be an easy load.  Two quick examples are electrostatics like Sanders or Martin Logan or the legendary Apogee Scintilla.   Electrostatic panels are essentially constructed like giant capacitors, so a 1/3 Ohm at the high frequency is not uncommon. 

The Apogee Scintilla, for instance, was essentially, a giant fuse, with a typical impedance around 1.4 Ohm as a result, and these speakers made Krell's amplifiers famous as they were some of the only amps capable of driving them.  A 50 Watt/channel Class A amplifier would deliver 400 Watts into each of them at 1 Ohm.  Fortunately later models were more reasonable around  3 Ohms. 

Sometimes designers do pull more current for more volume, but these are still typically well managed by most amps.  For instance, using 3 woofers in a single loudspeaker can lower the impedance.  Also, we often can pick 4 or 8 Ohm woofers and may pick to get better matching to a mid or tweeter.  The 4 Ohm version will play 3 dB louder thanks to the current doubling.

 

The Ugly 

There are three loudspeakers I want to show you as example of really questionable impedance curves.  To be clear, without taking a speaker apart it is impossible to know for sure what is going on under the hood, or whether this is an intentional "juicing" of the curve or a natural by product of good crossover design. 

The speakers are:

• Focal Profile 918
• Kef Reference 1 Meta
• Revel Ultima Salon 2 

 Ages ago I did a complete electrical tear down of the Focals.  What I found really disappointed me at the time.  I found a bank of resistors and caps which appeared to be there deliberately to lower the impedance.  Before we dive in lets look at a typical ported  speaker impedance curve. 

Here's an example of my own, the SNR-1, but almost ANY speaker in Stereophile with a port will be similar:

 

 

On the left are the typical dual impedance humps.  On the right is the impedance hump caused by the midwoofer to tweeter crossover.    The dual port and driver humps are expected and completely benign except for the weakest of amps.  

 Now that we know that, lets examine the speakers in order.  First the Focal Profile 918.  I actually simulated an alternate crossover for this speaker.  

 

The green curve is the original.  The second port resonance has almost vanished, and impedance remains under 4 Ohms  from 40 to 400 Hz.    At 95 Hz the impedance is about 2.3 Ohms.  A punishing impedance for many amps, and also completely unnecessary.  

The blue line is the simulated crossover improvement.  The second hump is restored with much better impedance below about 150 Hz.  For our three sample speakers this is the only one I have a schematic for.  

Notice the capacitor and resistor banks?  Completely unnecessary.  You greatly improve the impedance just by removing C2, and with an inductor change can remove the second bank of resistors.  These resistors are basically just here to steal power and heat up the interior of the speaker cabinet. Good thing it has a big port on the bottom! 

Now that we have at least one good example of how impedance curves can be juiced or altered by a crossover designer I want to turn to a modern and not so modern example which might have similar issues. 

 

KEF Reference 1 Meta

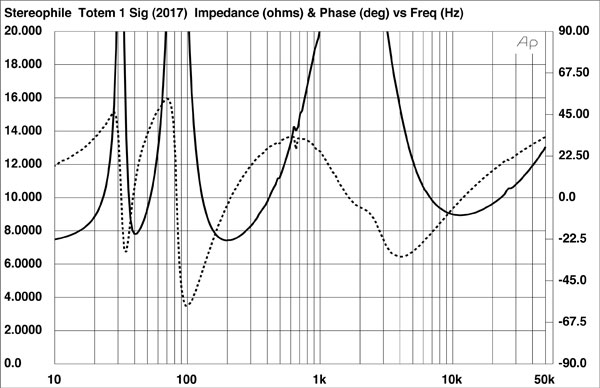
 The second speaker to cross my radar for possibly being deliberately demanding is the KEF Reference 1 Meta.  

This bookshelf speaker was released sometime around 2022 and we benefit greatly by a full write up from Erin's Audio Corner.   While Erin does note this is a very difficult to drive speaker due to a very low Equivalent Peak Dissipation Resistance (EPDR) of around 1 Ohm neither he nor any other widely published reviewer (which I'm not) mentions how odd the impedance curve is for a ported speaker.   

 

Notice that like the Focal, the expected second hump is missing.   We could ask "isn't this just an impedance flattening circuit? " Well, if it is then the fix is worse than the problem.

Revel Salon Ultima 2

While the Focal and KEF have been on the back of my mind for a while, it was over at DIY audio that the Revel and an important anecdote crossed my vision.  User cyclotronguy asserts: 

According to the Harmon engineers, they had specifically designed a loudspeaker that while it looked easy to drive on-paper , in fact was quite reactive and demanding so as to showcase the high wattage ML amps they were about to market.  

 

And it was that story, along with the impedance curve where it all clicked:

  

A very similar signature as the KEF.  Missing second hump, and hard to drive. 

Conclusion

I can't prove intention in any of these designs.  It is not wrong to say that these speakers are all going to be "discerning" of amplifiers because anything other than top level amps will wither under the stress. 

I can say that I don't know of a normal way the Focal speaker designers get to that schematic, or the KEF or Revel speakers end up missing a driver resonance hump.   My advice to any audiophile reading this though is to please, consider if you really want a "discerning" speaker, or one that's easy to live with.   It is my conclusion that in most cases you are going to enjoy more music more clearly and for less total cost of ownership with a less demanding speaker of the same type. 

 

I'm definitely not saying you should not by an ESL.  If that's what you want, go get it. I'm saying if you are deciding between a pair of dynamic speakers, please don't be tricked by this gimmick.   

Powering Woofer Mark I

 The front view of the Mark I.  The original SNR-1 is on top.  The twin 10" aluminum woofers sit underneath.  

Below is the rear view, showing the tweeter and mid-woofer connections on the back of the PW-1's cabinet.   Note that the bottom section has a 3-way Class D amplifier.  The speaker jacks on the bottom cabinet are amplifier outputs.   

 The SNR-1 were originally intended to be passive speakers but with an external crossover.  In this case, the removal of the external crossover and connection to the PW-I was trivial. 

The drivers are Dayton Audio RSS265HF-8.  They are 10" aluminum and in this sealed cabinet would do 40 Hz alone.  I had the choice of doing 1 10" woofer, ported to get to ~ 25 Hz, or 2 sealed and I went with sealed for the higher output, lower distortion, and lower group delay.  It did need a little boost in the DSP, but I have so much output available in my modest living room this was trivial.  Also, since this is now tri-amped I can afford to give the bass more power and still have another 250W for the mid and 100W for the treble. 

 

Here's a beauty shot of the woofers.

 

 

Tesla Cybertruck

 Dear Elon Musk:

 Please allow me to submit examples of how I can improve upon your design.

Built for comfort, not for speed:

 

Next, lets introduce a more affordable version.  Replacing the steel parts with cardboard is a sustainable option which makes it easy for owners to do their own repairs: 

 

The Complete Guide to Network Surge Protection for the Home

Many homeowners and apartment dwellers discover too late that their lovely surge strips were completely useless at protecting their computer and hifi gear from lightning when a surge has come in through a cable TV/Internet or antenna.  

Whats worse is that minor surges that don't cause visible, or olfactory evidence can still make your TV, PC or music streamer useless from damage to a $1 network part. 

Surge protection for your household outlets is critical but if that's all you do you are still vulnerable to surges from your Internet and Ethernet wiring.  We'll show you how to close these gaps. 

Full Disclosure

Doing the research for this blog takes time and effort and I justify it by using Amazon associate links.  Purchasing items linked on this page will probably make me a buck or two.  It is also true I personally use all off the approaches and most of the gear I link to. 

 

When you consider how much time and effort to take in protecting your home consider not just the cost to replace but the time and effort to replace, and whether you can live without the gear while fixing it.  My work PC and home office equipment for instance is not at all something I want to think about replacing.  My stereo receiver is 60 lbs and an absolute beast to take out of the rack, anything I can do to keep it from moving before I die is well worth it.   On the other hand, I have lived in the south near thunderstorm prone areas for about half of my life so the risk assessment for me may look more paranoid than for you. 

 

Perfect Protection

There's no such thing as perfect protection when it comes to lightning, or a car accident, but just like a like car accident our goal is to turn the majority of incidents into survivable events your gear metaphorically walks away from unscratched.  A better example may be a bicycle helmet.  A 5 MPH accident on a bicycle can cause lethal head trauma, but a helmet transforms most of them into situations where you brush yourself off, fix the chain and keep going. 

 

Network Surge Damage

Any copper wire that crosses the barrier from outside your home to inside can be a source of an electrical surge entering your home.  Electricity doesn't much know the difference between an Ethernet cable, copper pipe or your household wiring so once inside it will look for the easiest way to reach the earth.  This can be through network ports or a combination of network ports and AC wiring.  It's not uncommon for lightning to find multiple paths to ground either.  

 We are going to divvy up the areas we are concerned with into three zones: 

• The external outdoor/indoor interface
• The cable modem
• Indoor Ethernet wiring

Our working principle is to isolate and minimize potential damage caused by a surge attempting to find a path to ground via your home and electronic equipment. 

The Outdoor/Indoor Interface

When we think about how the Internet reaches our home there are several kinds of Internet service providers:

• Coaxial 
• Fiber
• 5G

Even homes with fiber service may have fiber terminated outside, with coaxial or Ethernet bridging the gap.  What we really care about is the cable, if any, used through from outside the home to inside. 

 

Non Metallic Internet 

If you have 5G or fiber optic cable coming through the wall you can skip this section and go onto the cable modem and indoor wiring sections.  5G and fiber cables are immune to surges. 

 

Coaxial Connections 

Outside of the home you want to use a gas discharge coax surge protector.  This is actually true for all your coax wires, including antennas on the roof, satellite dishes in the yard, etc.   These devices are imperfect, their job is to minimize the blast radius and also direct high surge currents to your ground rod OUTSIDE your home.   Mount it directly on the ground block outside, which is required by law for all coax cables coming in.

 

To be clear, a ground block is required by electrical code (i.e. the NEC) to ensure your home's ground (and by extension the neutral)  wires are at the same potential as the coax cable shield and prevent one type of dangerous situation but they are not surge or lightning protectors of any sort.   In particular it offers no protection against a high voltage being present on the inner conductor.

 

Coaxial surge protectors are not required, but allowed and IMHO necessary and the best place for them is on the outside grounding block. 

 

Be sure your surge protector is rated to 3 GHz and uses type F, which is the common household connector.   

 

The Details 

GDT discharge protectors are self-healing and high current.  The bad part is that they may not respond as fast as other devices with diodes or MOVs. The tubes inside will energize around 90V but because it may take a few picoseconds to activate you may end up with 800V-1000V inside for moments.  This will prevent the large amounts of surge current but that may be enough time to fry sensitive integrated circuits in the modem.  

The reason I'm so fond of pure GDT protectors outside despite this vulnerability is they rarely need to be replaced and can handle high currents safely.  If I'm going to have a 100A surge I want it to happen outside my home, not inside via the cable hidden in my walls.  

My personal experience was that when I first moved in I put a GDT outside and wired my modem to my wifi router with Ethernet.  We had a major storm in 2021 that took out the cable TV provider's equipment and every cable modem in my subdivision.  However in my home that's all it did.  The cable modem stopped working, but with no visible damage and no smell and my Wifi router worked perfectly.   Of all my neighbors I'm the only one with any Ethernet cables at all inside and I suffered no damage at all indoors. 

What about insertion loss?

Insertion loss means that putting anything in line with the coaxial signal may degrade the strength of that signal.  That's something to worry about, but gas discharge tube protectors are excellent in this regards, with very low insertion losses ( < 0.5dB) being typical.   I recommend that you go ahead and install one with this in mind and see if it causes you any problems.  If it does then you may be better off with post-modem surge protection, which we discuss below. 

 

Ethernet

If your fiber provider uses an Ethernet jack outside as the interface into your home  I suggest an Ethernet isolator, not a surge protector like this one.   Absolutely avoid Ethernet "surge protectors" with ground pig tails.   What matters here is the cable length.  If it's 2' from outside to the cable modem you can skip this.  If it's 20' you really should isolate.

 

The Cable Modem

If you are an apartment  I can pretty much guarantee your apartment complex does not have adequate lightning protection for the network distribution.   You may not be able to mount a coax surge protector on a ground block but it's not a bad idea to have one anyway attached to the modem.

If you have optical fiber coming in there's nothing you need to do, they are inherently immune to electrical surges. 

You should  put your cable modem on a surge strip.  This is important as lightning may enter the modem and then attempt to leave via the AC wiring, specifically the hot wire, damaging other gear on that same leg.   Tripp Lite makes a number of good models.  If you are particularly paranoid you might want to put the modem on it's own surge device, though honestly I put all of my networking devices on a UPS / Surge protector together. 

If you have followed all of my advice, above, you have protected your home and taken major steps to protect your network but the cable modem will still remain the most vulnerable.  Think of it as a sacrificial component in your multi-stage protection. 

The Details

Grounding surge protectors for Ethernet have been identified as causing damage to be more likely than without them.  The technical issue is that they may convert common mode surges to differential.  When that happens the downstream devices are 10-100x more vulnerable to damage.  Isolators tested to UL 60-601 are better.  We've seen very expensive isolators with TVSS we would recommend but ouch, the cost.  You are better off running fiber.  

 

Indoor Wiring

As we mention above, even with outdoor GDT suppressor and a surge strip some level of lightning surge voltage may still make it into the cable modem.  Once inside that surge could propagate through every other wire coming out of it all the way down to your home entertainment center and all those devices.   We want to add protection between the cable modem and your internal Wifi router.   For this reason we discourage the use of combined modem/routers if you plan to wire all your Ethernet cables to it.

 

There are two solutions here.  Use an Ethernet isolator, which we cover above, super simple.  Another is to create an air gap via the use of Ethernet/fiber converters which is what I do.   If you want to get super fancy you'd use an Ethernet/fiber converter along with a Wifi router with built in SFP+ port allowing you to go to your router directly via fiber.  Pay attention to the connector type, LC vs. SC before ordering SFP modules and cables. 

 

Personally I use a single Ethernet/fiber converter, a 1m fiber cable which feeds a home office router with built in SFP port which then short Ethernet to my Wifi router.  It's a work thing.   The point is that there is no metallic path from the outside coax to my indoor routers except via potentially the household AC wiring.

 

If you feel comfortable with either solution the fiber air gap is a better solution than the isolator.   It is also very much recommended if you want to place your wifi router at some distance from the cable modem.

Beware Long Ethernet Runs!

One last thing to be concerned with is the potential for an electromagnetic pulse (EMP) from a lightning strike to induce a surge in metals.  All the wiring in your home is susceptible to this and the longer it is the better of an antenna it will be.   If you have Ethernet cable runs in your walls of longer than 20' you should consider an isolator at the end, closest to your most expensive equipment.  I have two, one at my home office switch and one before my home theater's switch as well.   Of course, this leaves your wifi router vulnerable, so if you want to buy one for each end go ahead. 

 

Obviously, if you can afford it, running fiber inside your home for long runs is ideal.  

 

To be clear, our recommendations in regards to internal Ethernet wiring is that we cannot prevent the high voltage potential from an EMP, but we can attempt to isolate the damage.  It's better to fry a single Wifi router than to attempt to pull a high current surge through the wall to reach even more gear, and also still fry the router.  

 

Wifi Surges

One way in which Wifi is clearly superior to Ethernet is that  a wifi signal won't propogate an electrical surge.   Your phone or tablet, unless charging, will never get burned out because lightning entered your home via a cable modem and your wifi router.  It just won't happen, but your chargers are absolutely vulnerable to surges which can make it to the devices they are charging. 

 

Beware the use of an access point though.  If you use Ethernet to the basement and then use an access point to enhance your Wifi signal there make sure it's on a surge protector or you run the risk of the Ethernet providing a surge path to your basement AC.  

  

The Beginning After The End

I needed to post something about this anime because it's suddenly created a buzz to distract from just how bad it is.   It's so derivative even the title of the anime is derivative.

If you believe the online hype. viewers are upset over the animation quality.

 This misses the main problems: 

• We've all seen this story before
• We've seen this title before 
  
• Bad direction
• Slow burn

 

Viewers complaining about the animation quality fall into two camps: 

• Fanboys of the original web toons who already know all the hidden plot points
• Action freaks who wouldn't know a good plot if it slapped them awake.  

I simply cannot believe how much negative buzz this has generated.  I would not be surprised if it was revealed that anime and gaming sites are making money by covering the negative buzz and creating a perpetual motion hype machine.

And don't get me started with all the influencers who are using Solo Leveling as a foil to compare this to.  Come on man!! Solo Leveling might as well be watching mixed martial arts while this is a fishing show.  So far apart that to even bring up SL is laughable but almost every damn web blog (including this one) has to say it:  Sorry this isn't Solo Levelling.  Damn right it's not.  😂

 TBATE is yet another isekai of a boring dude who is reborn to be just too precious.  Is that what middle aged men in Japan aspire to?  Being reborn a 12 year old in capris?  Instead of Solo Leveling we should compare it to  As a Reincarnated Aristocrat, I'll Use My Appraisal Skill to Rise in the World.   I'll leave it to others to debate which is better.  Spoiler alert:  They both suck.